(Euclide, auteur des Eléments)

par Christian Velpry

Une affaire qui se déroule sur un long espace de temps et où l’on voit se produire expropriation, humiliation, effacement du nom, d’un côté, appropriations abusives de l’autre.

Présentation, émergence d’une problématique

Les notes et remarques ici présentées s’inscrivent dans une critique plus générale de ce qui est dit par les Modernes de la science grecque (antique).

Dans presque tous les ouvrages contemporains sur l’histoire de la science antique, on lit des phrases aussi étonnantes que : « Les peuples anciens avaient déjàune certaine pratique empirique des sciences, avec les Grecs commence l’esprit d’abstraction » (souligné par moi). A ma connaissance, seul Abel Rey a su résister à la tentation d’écrire quoi que ce soit de semblable. Or, au moment où une telle opinion s’affiche, on dispose, d’un côté, des écrits de Platon et d’Aristote, qui reflètent exactement le niveau atteint par les Hellènes de leur temps, et, de l’autre, de textes retraçant une partie au moins des performances scientifiques des savants d’Égypte et de Mésopotamie.

 

Mais je viens à l’histoire d’Euclide et à la place qu’il occupe dans la culture. Le texte de ses Élémentsconstitue, au moment où il est produit, une refondation des mathéma­tiques. Oubliant ce qui le précède, la descendance, jusqu’à nos jours, voudra le prendre pour une fondation. En même temps les historiens occidentaux prétendent l’agréger à la tradition hellénique.

L’ouvrage est relativement bien daté : il est « dédié à Sôter ». Ce nom est le titre que prend le premier Ptolémée en 306 av. J.-C., avant de quitter le pouvoir en 285 (et de mourir deux ans plus tard) ; cela donne les dates limites pour la publication. L’ensemble de l’œuvre d’Euclide, qui était très vaste, est presque entièrement perdu, mais est très bien attesté par la descendance immédiate, Archimède de Syracuse, puis Apollo­nios de Pergè, notamment. Ceux-ci donnent sur l’œuvre une foule de détails précis, révélant aussi le statut pris par l’auteur.

Sur l’homme Euclide, presque aucun renseignement. Quand une œuvre entre dans l’histoire, mais que son auteur n’y entre pas, il est légitime de se poser des questions.

 

Un grand hiatus

La conquête alexandrine est un moment de changement assez brutal. Les Égyptiens, comme d’autres peuples, perdent définitivement leur indépendance et passent sous la domination coloniale des Hellènes, conduits par leur chefferie macédo­nienne. Parmi les biens dont les nouveaux maîtres vont s’emparer, la science. Une des vertus de la science est son aptitude à la transmission, elle est donc faite pour être reprise, toutefois ce qui va se produire est que le peuple conquérant va vouloir s’attribuer tout le mérite dû aux auteurs appartenant aux peuples conquis, allant jusqu’à ne pas retenir leur nom, ou, pour les plus importants, leur conférant un surnom pris dans le corpus grec.

Comme je l’ai évoqué, les textes de Platon et Aristote donnent l’étiage de la science hellène juste avant la conquête alexandrine. Et les Éléments d’Euclide sont publiés au plus tard trente-sept ans après la mort du Stagirite. L’énorme saut que représente le surgissement de cette œuvre ne peut pas être accompli dans un laps de temps aussi court. Totale impossibilité. Donc la rattacher à la tradition hellénique est strictement impossible.

Remarquons une différence de méthode : si nous entrons dans les textes, nous voyons qu’Euclide va résoudre des questions déjà posées chez Aristote, par exemple au sujet de la somme des angles d’un triangle, mais Aristote juge encore de la vérité d’une proposition en « inspectant la figure » (Aristote, philosophe du « voir »), chez Euclide, on apprend à « raisonner juste sur une figure fausse » (selon l’excellente caractérisation apparue plus tard) et la preuve est établie au terme d’une progression par le discours : la preuve est logique. La géométrie désormais s’entend plus qu’elle ne se voit.

Un détail sémantique intéressant : le point, en géométrie, chez Aristote, c’est stigma (latin : punctum, français : point, c’est-à-dire piqûre), chez Euclide, c’est sēmeion, c’est-à-dire signe, signal, étiquette. On étiquette une localisation précise, et on lui donne un nom (A, B, etc.) pour pouvoir s’en saisir par le langage : on dira « le triangle ABC ». Mais il est clair qu’avec Euclide on atteint à un autre niveau d’intellection, beaucoup plus évolué. D’ailleurs la logique pratiquée par Euclide, et que méprisent systématique­ment les historiens de la Logique mathématique, qui s’extasient sur celle d’Aristote, présente une avancée énorme par rapport à cette dernière, et même par rapport à celle des Mégariques, élèves d’Euclide de Mégare.

C’est en Égypte principalement que l’on trouve la fondation de la géométrie. Déjà au XIXe siècle av. J.-C., le document reproduit dans le papyrus Golenischev, qui se révèle avoir été la copie d’examen d’un élève scribe, contient la preuve que les maîtres avaient atteint un niveau de performance étonnant en mathématique : on y trouve le calcul du volume d’un tronc de pyramide (carrée) et celui de l’aire d’une demi-sphère. Ces calculs ne peuvent être établis que par des voies théoriques, qui ne sont nullement élémentaires, même aujourd’hui. La doxographie de Démocrite fait comprendre, du reste, que la preuve théorique ultime de ces calculs a été donnée en Égypte de son temps (Ve siècle) ; elle résulte de procédés infinitésimaux dont c’est l’attestation explicite la plus ancienne.

L’œuvre d’Euclide se trouve en continuité avec la mathématique égyptienne.

 

Sur l’homme Euclide, peu de renseignements ; curieusement, c’est à la Renaissance que surgissent des questions à son sujet. Et la réponse, bien curieuse, est qu’il était grec, c’est-à-dire hellène. Comment un homme qui a produit une œuvre aussi énorme, et immédiatement référencée, a-t-il pu disparaître au point qu’on ignore sa cité de naissance, et le nom de ses père et mère ? Si Euclide est un Hellène, c’est impossible : on connaît bien « l’état-civil » de Platon, Aristote, Archimède, et de tous les grands (d’époque historicisée). Euclide : néant. La conclusion s’impose : il n’est pas hellène. Mais, comme ses contemporains et descendants immédiats devaient savoir assez exactement d’où il sortait, si la société alexandrine a décidé de ne pas transmettre ces données, cela constitue justement une indication. Il est clair que c’était un « colonisé » : et vu son statut scientifique, ce ne pouvait être qu’un prêtre égyptien, assez probablement mélanoderme, comme le grand nombre des Égyptiens à l’époque.

 

Les mésaventures d’Euclide dans l’âge moderne

1. Le blanchiment d’Euclide

Il nous faut revenir sur la colonisation alexandrine. Déjà, avant elle, les pharaons égyptiens, après les épreuves subies des Akkadiens, s’étaient livrés à une politique philhellène très nette depuis le début de la XXVIe dynastie : au VIIe siècle, Psammetik Ier ouvre aux Hellènes le comptoir de Naukratis ; il accueille dès ce moment les fils de l’aristocratie grecque dans des écoles situées aux portes des temples et où des maîtres égyptiens enseignaient leurs élèves en grec. Les Hellènes n’ont jamais pu apprendre l’égyptien, un certain nombre d’Égyptiens ont appris le grec.

Il n’y a donc rien de surprenant à ce que l’Égyptien Euclide maîtrise parfaitement le grec, en lequel il transmet son œuvre. Quant au nom Euclide, il l’a reçu dans l’entourage royal car il a été l’objet, comme tous ceux qui à un titre ou un autre intéressaient le pouvoir, de la considération du prince (cf. anecdotes rapportées par Proklos).

Je fais une remarque sur les noms et les citations : Apollonios de Pergè a travaillé, on le sait de diverses sources, avec les propres élèves d’Euclide ; les quatre premiers livres de son grand ouvrage, les Coniques,reprennent, de son propre aveu, les Éléments coniquesd’Euclide (ouvrage aujourd’hui perdu). Dans les dédicaces et avant-propos de ses livres, Apollonios cite des noms, exclusivement helléniques ; il est possible que certains noms soient portés par de non-Hellènes, mais on ne peut guère penser que figurent dans la liste ceux des élèves d’Euclide avec qui il a travaillé. Ces derniers, de stature plus modeste que leur maître, n’avaient sans doute pas reçu de nom grec, donc ils ne méritaient pas l’honneur d’une citation…  Ne retrouve-t-on pas ici le canevas des mœurs coloniales ?

Voilà donc ce qui reste des noms égyptiens : rien. Or, les hommes de science étaient, en grand nombre, égyptiens. Plus tard encore, il ne faut pas voir en un Claude Ptolémée, né à Ptolemaïs, en un Plotin, né à Assiout-Lycopolis, autre chose que des Égyptiens.

Alors d’où vient que nous nous permettions de les prendre pour des Grecs ?

Pour Euclide, je crois pouvoir révéler l’ultime étape de « l’assimilation ».

 

Récit. En 1482, à Venise, Eberhardt Ratdolt décide de donner la première édition imprimée des Éléments. Il va choisir pour cela la version de Campanus, datant du XIIIe siècle, compilation des traductions latines des traductions arabes de l’œuvre. Il reprend fidèlement le texte, mais commet un écart sur le titre. Campanus avait inscrit : « Euclidis Elementorum quindici libri » (quinze livres d’Éléments d’Euclide), Ratdolt imprime : « Euclidis Megarensis Elementorum quindici libri », apposant au nom d’Euclide l’ethnique « Megarensis » et l’assimilant donc à Euclide de Mégare, déjà nommé. Ratdolt a endossé une grave respon­sabilité en agissant ainsi. Comme ce fut le premier ouvrage de science jamais imprimé, cela constitue aussi un présage inquiétant pour les relations entre la science et l’imprimerie.

En 1576, le jésuite Clavius va se sentir gêné par le coup de Ratdolt : faisant éditer une version latine, d’ailleurs fort intéressante[1], après édition des manuscrits grecs, et rappelant les textes récemment retrouvés de Proklos de Lycie, qui situaient très précisément Euclide en relation avec le premier Ptolémée, il se contente de déclarer qu’Euclide auteur des Éléments n’était pas Euclide de Mégare mais « un autre, vivant du temps de Ptolémée ». Ratdolt peut-être, Clavius sûrement, savaient que notre Euclide était égyptien, mais le jésuite s’est bien gardé de faire le rétablissement complet de la vérité. A l’époque, je le rappelle, le mouvement « humaniste » avait posé comme principe que les « Grecs », c’est-à-dire les Hellènes, étaient nos ancêtres culturels, et, en dépit d’une soif renouvelée de connaissances, ils affirmaient que toute la pensée venait d’eux, ou à la rigueur des Hébreux et de la Bible. Naissance contemporaine de l’impérialisme et de l’esclavagisme (au sens moderne) : on connaît le document accablant qu’est la fameuse lettre du pape Nicolas V, datée de 1454, document autorisant, « au nom de Notre Seigneur Jésus-Christ », la colonisation, le baptême forcé et la traite. Tenir d’un Égyptien, probablement nègre, la source de la science était devenu alors insupportable : sans se gêner, ceux qui s’étaient désignés eux-mêmes comme Humanistes l’ont blanchi.

 

2. Quelques mots de géométrie, autour du 5^e postulat

Nous allons quand même parler un peu ici de géométrie et de logique. Un tournant se dessine vers 1825, lorsque J. Bolyai et N. Lobatchevsky vont apporter LA contribution décisive, qui  sera complétée par celle de Beltrami en 1868.

Le 5^e postulat de la Géométrie, encore appelé « postulat des parallèles » (cf. infra), est une chose qui a fait couler beaucoup d’encre, sans discontinuer, de sa naissance à nos jours. Euclide est un des premiers, peut-être le premier, à avoir fixé la forme des traités mathématiques, où, s’appuyant sur définitions et postulats donnés en tête, il est démontré une suite ordonnée de théorèmes, la démonstration de chacun ne faisant appel qu’aux définitions et postulats ainsi qu’aux théorèmes antérieurs. Se trouvent clairement exclus, par ce moyen, les cercles vicieux. Une telle structure est implicitement décrite par le titre, Stoikheia (Éléments) ; en effet le terme « stoikheion » désigne en grec l’élément d’une suite ordonnée (dès avant son usage mathématique l’expression plurielle « ta stoikheia » désigne « les lettres » de l’alphabet, ou tout simplement « l’alphabet »).

Il y a eu, dès l’Antiquité, des interrogations sur le statut de postulat. Est-ce que l’énoncé d’un postulat doit être considéré comme une vérité ou non ? Quelle différence entre « axiome » et « postulat » ? « Axioma », terme très aimé d’Aristote, signifie un énoncé vrai par lui-même, validé, reçu ; en face, on a « aitēma » (déjà défini chez Aristote), dont le sens est « demande », d’où sa transcription latine, « postulatum » : un aitēma joue dans une théorie le même rôle qu’une hypothèse dans un problème ; c’est un énoncé qu’on demande au début, pour pouvoir en déduire d’autres, les théorèmes : il n’y a pas, dans le terme, de connotation signifiant vérité ; c’est simplement un de ces premiers énoncés dont on va déduire les autres. Le travail de Bolyai et de Lobatchevsky a consisté à prendre les mêmes prémisses qu’Euclide pour la géométrie, sauf à remplacer le 5^epostu­lat par sa négation[2] : ils n’ont pas, ce faisant, nié une vérité, ils ont seulement inversé un postulat. Leur réussite a contribué à justifier Euclide d’avoir appelé cet énoncé postulat, ce qui avait été contesté dès l’anti­quité et jusqu’à leur contribution. Ainsi ils partent du même tronc qu’Euclide, à partir d’un point ce dernier développe une branche, et eux ont développé une seconde branche, complétant un Y, si l’on peut dire. Gauss, mathématicien génial par certains traits, déce­vant par d’autres, ayant trouvé les mêmes résultats, a fait obstacle à l’émergence de cette géométrie ; il l’a nommée « non euclidienne », terme regrettable puisque le travail d’Euclide en amont de l’emploi du 5^e postulat, en dessous des branches de l’Y, peut aussi bien être appelé « non euclidien » ! Euclide est le fondateur de la « géométrie non euclidienne ». Voilà un résultat verbal montrant le caractère vicieux de la dénomination.

Euclide v/ Gauss : Euclide est le premier à avoir compris que le carré n’existe pas, ou du moins qu’il faut préciser des conditions pour pouvoir démontrer son existence. La géométrie antérieure à Euclide (et dans toutes les aires civilisationnelles) repose sur l’évidence non remise en cause du carré et du rectangle. Il ressort d’une analyse du texte même des Éléments, qu’Euclide fut le premier à mettre en cause cette évidence, ce qui l’a conduit à bâtir sa géométrie sur la théorie du triangle le plus général, et à adopter le 5^e postulat pour donner une existence légitime au parallélogramme, au rectangle et au carré.

Le premier livre de la Géométrie contient d’abord les résultats les plus généraux, avant de passer à ceux dépendant du 5^e postulat. Construction magnifique : vingt-et-un siècles d’avance sur la pensée mathématique occidentale.

 

3. Sur la théorie des rapports incommensurables, témoignage de Platon

On trouve, dans l’Antiquité deux théories des rapports incommensurables, une première, encore assez élémentaire, est celle qui envisage le rapport de la diagonale du carré à son côté, et des problèmes du même ordre. Les Pythagoriciens avaient déjà abordé ces problèmes, qu’on voit affleurer chez Platon en plusieurs dialogues : dans le Ménon, Socrate aide le serviteur à « se ressouvenir » et démontrer enfin que le carré construit sur la diagonale est le double du carré donné. Ainsi l’on remarque que la diagonale et le côté du carré ne sont pas commensurables, mais que les carrés construits sur ces longueurs le sont, eux : on dit alors que ces longueurs sont « commensurables en puissance » (« dunamei summetra », en grec). C’est à un niveau plus élevé de difficulté que l’art a consisté à affecter un rapport à des grandeurs sous la seule condition d’être de même espèce (« homogènes ») : là, on perd le calcul arithmétique, il n’est plus question de carrés ou autres « puissances » (au sens mathématique). La théorie est plus fine et renvoie à des procédures infinitaires. C’est cette théorie forte des rapports incommensu­rables qu’on trouve au 5^e Élément d’Euclide, alors que l’autre est incluse dans le 10^eÉlément. On peut penser qu’Euclide a amélioré la théorie qu’il donne au 5^e Élément, mais il n’en est pas l’inventeur.

Le fait que je vais mettre en cause ici est l’attribution de l’invention à Eudoxe de Cnide faite par les Occidentaux à la fin du XIXe siècle. Peu avant, les Occidentaux étaient parvenus à une définition enfin complète des « nombres réels » ; deux voies ont été trouvées pour la « construction des nombres réels », le procédé de Méray (1868) et celui de Dedekind (1873). Ce qu’ils ont obtenu reprenait finalement le travail donné par Euclide au 5^e Élément, mais en le complétant par la considération de la continuité, absente chez le géomètre alexandrin.

La proximité de leur travail avec celui d’Euclide, faisant resurgir le nom de ce dernier, a dû incommoder encore pas mal de gens. Toujours est-il que c’est dans les décennies suivantes que les historiens des sciences ont mis en avant le nom d’Eudoxe comme inventeur de la théorie forte, dans l’Antiquité. Or ceci est encore une falsification, dont je note qu’elle est contemporaine du Congrès de Berlin, où les Occidentaux décident du dépècement de l’Afrique.

Déceler cette falsification est simple : il suffit de se donner la peine d’aller lire, dans les Lois de Platon, le passage indexé 817-e à 822-c. Platon, sous l’identité de « l’Étranger athénien » va secouer durement, dans ce texte, non seulement les Athéniens ses concitoyens, mais aussi les Hellènes ses compatriotes au sens large. Avant de faire prononcer des propos ineptes, du point de vue scientifique, à ses nobles hôtes Megillos et Kritias, il désigne l’Égypte comme le modèle sur lequel les Hellènes doivent d’urgence s’appuyer s’agissant des trois disciplines de l’arithmétique, de la mesure des grandeurs géométriques et de l’astronomie…

(819 a) Autant donc de chacune [de ces disciplines], faut-il dire, ont besoin d’apprendre les hommes libres, que la troupe nombreuse des adolescents en Égypte apprend aussi, en même temps que les lettres.

Donc la théorie des incommensurables évoquée aussitôt après est déjà enseignée dans les écoles scribales lorsque Platon est à la fin de sa vie.

L’erreur commise par Kritias au sujet des rapports incommensurables n’est pas aussi honteuse, à mes yeux, que Platon ne le chante, mais celle sur l’astronomie, à la fin du passage, paraît plus sérieusement accablante pour « la science grecque » : la culture astronomique des Hellènes, près d’un siècle après l’adoption du calendrier mésopotamien du Saros (cycle de dix-neuf années, incluant un calcul précis des éclipses de lune), reste désolant : le terme « planète » en témoigne encore, puisque son sens propre, usité au temps de Platon, signifie « [astre] errant ».

Mais je viens à la théorie des incommensurables. Platon ne va pas la décrire, la détailler mathématiquement dans ce texte. Mais il y a un mot, juste un mot qui oblige à comprendre que la théorie évoquée est celle que l’on va retrouver dans le 5^e Élément d’Euclide, la théorie forte. En effet, Platon va parler de grandeurs « mesurées » (grec « metrēta ») et de grandeurs « sans mesure » entre elles (grec « ametra »). Cette terminologie est caractéristique de la théorie forte, en effet dans la théorie faible il s’agissait de « commensurables », ce qui correspond à « mesurées », et de « commensu­rables en puissance », ce qui ne peut pas se retrouver sous le terme « ametra ». Ce seul petit mot suffit à nous donner l’assurance que la théorie forte était celle dont Platon parle ici.

 

Les historiens du XIXe siècle ont forcé le sens d’un passage d’Archimède qui désigne Eudoxe comme l’introducteur de la théorie. A-t-on le droit de le dire inventeur pour autant ? Pour évaluer l’attestation de Platon, je vais mettre une des phrases suivantes du passage en rapport avec des indications de Strabon et de Diogène Laërce :

(819 c) Ô cher Klinias, de toutes [ces questions] n’ayant moi aussi entendu parler qu’assez tard, devant ce qui à ce sujet nous affectait je fus étonné, même j’ai trouvé cela non pas humain mais plutôt [le fait] de porcs à l’engrais, et j’en ai eu honte non pour moi seul mais aussi pour tous les Hellènes. 

Diogène évoque ce qui est très certainement le premier voyage d’Eudoxe en Égypte, sous le règne de Nectanébo Ier (379-363) ; Strabon, lui, a interrogé les prêtres d’Héliopolis, dont les prédécesseurs avaient reçu Platon et Eudoxe (in Géographie, 17). La jonction, dans le texte de Strabon, de leurs deux noms laisse penser qu’ils ont dû, au moins une fois, venir ensemble. C’est forcément dans la vieillesse de Platon que cela a eu lieu, à quoi le mot « tard » dans la phrase de Platon fait écho. Cet ultime stage de Platon et Eudoxe à Héliopolis n’a pas dû durer autant que ceux de leur jeunesse, Strabon mêle peut-être des événements en évoquant sa durée. Néanmoins je crois significatif le rapprochement des deux noms donnés par le prêtre. C’est donc à ce moment que Platon et Eudoxe ont été initiés à la nouvelle théorie, qui devait être assez récente alors (la doxographie de Démocrite n’y fait pas allusion), et c’est le second, plus véritablement homme de science que le premier, qui a dû la diffuser en Hellade. La datation d’Eudoxe pose encore problème de nos jours : dans l’hypothèse de datation haute, il serait mort avant Platon, ce qui pourrait faire comprendre l’urgence qui saisit ce dernier dans le passage cité.

Mais il faut dire un mot aussi des « porcs à l’engrais ». Qui peut bien être concerné à la fois par les porcs et par la mathématique ? Énigme. Une réponse s’offre pourtant : les Pythagoriciens. Pythagore avait étudié longuement en Égypte, sous le règne d’Ahmosé/ Amasis, il avait atteint un grade élevé dans la prêtrise ; revenu en Hellade, il était resté fidèle à ses engagements, à la fois religieux et scientifique ; il est attesté qu’il se lavait cinq fois par jour, avait la tête rasée, se vêtait de lin, avait une nourriture végétarienne, et enfin qu’il fréquentait les seuls temples où ne se pratiquaient pas de sacrifices d’êtres vivants. Ses disciples étaient soumis à une discipline moins stricte, mais le porc était pour eux impur, comme pour les Égyptiens, alors qu’il ne l’était pas pour les autres Hellènes. Les pythagoriciens étaient ceux qui assuraient, si j’ose dire, le service de la science en Hellade. Or depuis la mort du maître, ils s’étaient peut-être un peu reposés sur leurs lauriers, omettant même de garder le contact avec leur « frères spirituels », les Égyptiens. Je pense que la phrase sur les « porcs à l’engrais » sont une pique destinée à réveiller ces dormeurs, et leur rappeler de revenir s’abreuver à la bonne source.

Ainsi nous pouvons écarter Eudoxe et rendre ce qui leur revient aux Égyptiens.

 

4. Axiome ou postulat

Je reviens une fois encore au terme de postulat, en laissant maintenant de côté le thème proprement géométrique, mais pour m’interroger sur les curieuses errances sémantiques des mathématiciens. Il semble que, depuis l’Antiquité, les difficultés théoriques liées au 5^e postulat d’Euclide aient ébranlé la fermeté des conceptions méta-mathéma­tiques[3] des spécialistes. Déjà des manuscrits anciens des Éléments, par une infidélité à l’auteur, rangent le 5^e postulat parmi les axiomes. C’est sur des éditions dépendant de ces manuscrits que vont travailler Bolyai et Lobatchevsky, chez qui le fameux postulat s’appelle « Axiome 11 ». L’erreur est seulement dans la désignation, puisque, sous leur plume, cet « Axiome 11 » prend bien valeur de postulat.

Avec le grand nombre des mathématiciens, qui font en principe très attention au langage qu’ils utilisent, ils ont manqué à prendre garde qu’ils utilisaient les termes « axiome » et « postulat » en dépit du bon sens, précisément du sens toujours conservé dans la langue. C’est ce caractère critiquable, chez les spécialistes des sciences exactes, par lequel ils se sont habitués à s’écarter du sens commun et se sont portés jusqu’à la maladresse de commettre des erreurs sémantiques dans la science et la méta-science elles-mêmes[4].

Quand on lit chez Jules Houël, préfaçant en 1867 Lobatchevsky : « Le travail remarquable dont nous donnons ici la traduction n’a de commun que le titre avec les nombreuses élucubrations des auteurs qui […] se sont éfforcés, sans beaucoup de succés, de démontrer à priori l’axiome XI d’Euclide, plus connu sous le nom impropre de postulatum », on reste stupéfait devant les derniers mots, on se demande même si Houël a porté attention au texte retrouvé et traduit par Peyrard au début du siècle. Il contribue à renforcer les deux erreurs de vocabulaire transmises par Bolyai et Lobatchevsky. Poincaré par la suite va faire de louables efforts pour réintroduire le terme de postulat, efforts qui resteront ignorés de Hilbert.

Mais ceux que j’accuse pour la grande responsabilité qu’ils ont assumée, et qui me paraît plus grave encore que celle de leurs prédécesseurs, ce sont les Bourbakistes. En effet, inaugurant en 1935 leur grandeœuvre, vouée prétendument à refonder les mathématiques (et qui s’accroît sans cesse, jusqu’à nos jours), ils l’appellent Éléments moins par fidélité à Euclide que par décision de lui tourner définitivement le dos en rebâtissant les mathéma­tiques sur des prémisses ne devant rien au grand devancier. Ils avaient donc le moyen, dans cet esprit refondateur, de revenir au sens exact des termes : ils auraient dû, à mon sens, en finir avec l’emploi détourné des mots « axiome » et « postulat » et affirmer tout à fait clairement que la mathématique se construit sur des postulats. De ne l’avoir pas fait, il résulte qu’ils se sont mis dans une sorte de mensonge initial, acceptant de s’inscrire dans la triste mode de « tromper la langue » ; il en résulte d’ailleurs un désavantage et pour les hommes de science, et pour les autres, le grand nombre des personnes qui, sans en être spécialistes, s’intéressent à la science. Cette faute pèse sur toutes les approches occidentales de la critique de la science.

Or sous les atteintes portées à la langue il est toujours à déceler une charge politique (cf. Paule Pérez, « Rien ne va plus chez les Yahoos », tm 8). Ce malentendu sur un terme euclidien est assez clairement suspect, il suffit d’en faire la remarque. J’invite tous et chacun à revenir au juste emploi des termes. J’espère voir bannir axiomeet axiomatique des emplois à contresens qu’on leur a imposés : on peut revenir à postulat, ou à demande(comme fait Peyrard), ou encore franciser en étème le grec aitēma. Cela suggère même de remplacer le malsonnant axiomatique : je propose de lui substituer un néologisme moins dur à l’oreille et plus facile à articuler,étématique.

 

Pour conclure

Il y avait assurément, dès l’époque d’Euclide, une difficulté propre à la théorie géométrique, et résultant du fait qu’elle jette un pont entre l’espace réel et le discours logique. Cette difficulté n’est pas rien, et il a fallu plusieurs millénaires pour la résoudre. Ceci étant, on doit remarquer que la première difficulté est issue d’une relative surdité des héritiers hellènes d’Euclide devant ce qui reste son invention la plus profonde : on note déjà alors une certaine difficulté dans les échanges culturels et scientifiques au temps de la colonie alexandrine. Quant à celles qu’on retrouve dans l’âge moderne, et qui subsistent aujourd’hui alors qu’au plan scientifique la question est désormais réglée, il y a lieu de les caractériser : les erreurs continuées des mathématiciens et historiens des sciences, sont liées à la hantise qu’on a d’évoquer les maux et les crimes de la colonisation ; l’interdit sur le nom d’Euclide, celui sur le terme de postulat, dû à la contagion, sont des marques typiques de ce que l’inconscient de la société refoule et qui, par nécessité, ressort toujours, refusant de se laisser oublier.
C. V.

 

 

Références

– les Éléments d’Euclide, traduits par F. Peyrard (Paris, 1819), rééd. actuelle Blanchard, Paris ;

– la traduction anglaise de T. L. Heath (1908) desÉléments est disponible dans une agréable présentation sur le site

http://cs.clarku.edu/~djoyce/java/elements/elements.html;

 – Euclide l’Africain ou la Géométrie restituée, de Christian Velpry, Paris, Menaibuc, 2004.

 

Né en 1937, Christian Velpry est heureux de sa venue au monde, mais considère que ses milieu, heure et lieu de naissance ont constitué pour lui une première erreur de casting. En 1940, il perd son père, tombé à Dunkerque. De ce manque s’élabore chez lui vers quatre ou cinq ans, un regard distancié et inquiet sur la société « qui fait des guerres où meurent les papas ».

En dépit de ses efforts et de quelques succès (agrégation de mathématiques à 22 ans, suivie de l’obtention d’un poste d’enseignant-chercheur à l’Université qui deviendra Paris 7), de l’intérêt qu’il prend à l’enseignement, de sa joie à s’engager dans la paternité (une fille lui est née), la faille entre la société et lui n’a fait, au double plan professionnel et personnel, que se creuser et s’élargir.

A l’université, conjuguant des connaissances et aptitudes multi-disciplinaires, concernant notamment l’Antiquité, il a créé un enseignement peu commun en Histoire des Mathéma­tiques. Ayant pu enfin produire des résultats de recherche surgis après sa rencontre avec des Africains, visités chez eux  — son hommage à Euclide en témoigne — il n’a réussi qu’à s’aliéner définitivement, par la mise en cause, qui s’y inscrit, de son milieu professionnel, la quasi-totalité de ses collègues. lI est de ceux, peu nombreux, qui ont tenu une position “résistante” en en payant le prix.

 

 

Note complémentaire

Énoncé du 5^e postulat, en traduction française :

[Soit demandé que] si une droite rencontrant deux autres droites fait avec elles des angles intérieurs d’un même côté inférieurs à deux droits, les deux droites, prolongées à l’infini, se rencontreront [du côté où les angles sont inférieurs à deux droits]. (Les mots entre crochets, superflus, sont peut-être une interpolation.)

Quelques explications sont nécessaires. Pour l’expression « tels angles sont inférieurs à deux droits » on doit entendre que le pluriel vaut addition, cela veut donc dire que la somme desdits angles est inférieure à deux [angles] droits (nous disons de nos jours 180°, mais Euclide ne connaît comme unité de mesure angulaire que l’angle droit, en abrégé « un droit », grec « orthē [gônia] » ; rappel : la [ligne] droite, c’est « eutheia [grammē] »).

Donnons une figure pour aider à saisir le sens de l’énoncé :

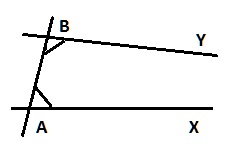
si la droite AB rencontre les droites AX et BY en faisant les angles marqués en A et B (qui sont d’un « même côté » de la droite AB et situés « à l’intérieur » des droites AX et BY)  et que la somme de ceux-ci soit inférieure à deux droits, alors le postulat énonce que les droites AX et BY suffisamment prolongées (« à l’infini ») se rencontreront.

A noter que le point de rencontre peut se trouver bien loin, en dehors de l’épure, n’importe où jusqu’à l’infini ; et justement la propriété de cet énoncé et de ramener une problématique globale, et incluant une recherche jusqu’à l’infini, à un contrôle local : on mesure les angles en A et en B, on fait la somme et on la compare à deux droits : l’énoncé assure, si elle est inférieure, l’existence du point de rencontre. L’énoncé du postulat est, notons-le, une implication.

 

Examinons maintenant ce que signifie la négation du postulat (supposée donc par Bolyai et Lobatchevsky) : elle affirme le contraire, c’est-à-dire que ladite implication est fausse, autrement dit qu’il existe un contre-exemple, c’est-à-dire un cas de figure dans lequel, bien que la somme soit inférieure à deux droits, les droites ne se rencontrent pas.

(Attention, la négation, en logique mathématique, ce n’est pas n’importe quoi !)

Ce nouveau postulat, négation du précédent, étant posé, Bolyai et Lobatchevsky (qui, pour le rappeler, n’ont jamais entendu parler l’un de l’autre, travaillant en même temps, l’un à Temesvar, l’autre à Kazan) ont précisé la nouvelle définition qu’il est bon de donner du parallélisme des droites ; supposons que, dans la figure, on fixe la droite AX et le point B, mais qu’on fasse varier la droite BY autour de B : pour certains angles, elle va être sécante à AX, pour d’autres non, de la façon exigée par le nouveau postulat. Il va y avoir un angle limite, correspondant, d’un côté, à la position d’une droite qui ne coupe pas AX, mais telles que toutes celles qui sont dans un angle plus serré, vers AX, coupent cette dernière : c’est cette non-sécante limite qu’on appelle, depuis Bolyai et Lobatchevsky, la parallèle à AX du côté en question ; mais il y en a une autre, de l’autre côté, donc la propriété de parallélisme devient orientée : deux droites sont parallèles dans un sens (et alors non dans l’autre) et par un point hors d’une droite passent deux parallèles à celles-ci, l’une dans un sens, l’autre dans l’autre. De plus, la propriété d’équidistance de la géométrie usuelle, n’est pas conservée : dans la direction de leur parallélisme deux droites se rapprochent asymptotiquement, c’est-à-dire que quand un point de l’une tend vers l’infini, dans la direction du parallélisme, sa distance à l’autre droite tend vers zéro. Tout cela se démontre. Les configurations obtenues sont étonnantes pour ceux qui ne sont habitués qu’à la géométrie classique.

Sur la figure ci-dessous, correspondant à la géométrie de Bolyai et Lobatchevsky, BY est parallèle à X’AX dans le sens de l’infini côté X, BZ est parallèle à X’AX dans le sens de l’infini côté X’. Dans l’angle en B qui « regarde » la droite X’AX passent les sécantes, et les droites passant par B dans l’autre angle ne sont ni parallèles, ni sécantes à X’AX : on dit qu’elles en sont « divergentes ». La figure est un schéma qu’il ne faut pas prendre comme figure « réelle », ce qui permettrait aux Aristotes d’objecter que « l’on voit bien » que BY et AX vont se rencontrer.

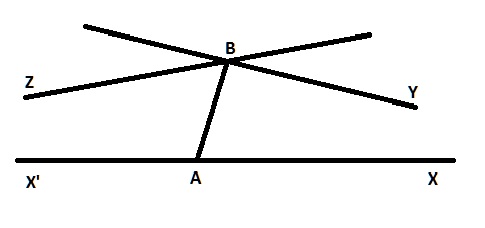
Le 5^e postulat a posé problème aux gens par le peu de prix qu’ils attachaient à la logique et au sens du terme postulat, d’une part, et par le fait que l’espace sensoriellement construit par les humains ressemble assez à celui de la géométrie classique. Si l’on reste étonné devant l’acquis de Bolyai et de Lobatchevsky, on peut l’être encore plus devant le fait qu’Euclide lui ait par avance réservé une place. Il faut dire aussi que pour opérer les calculs en géométrie de Bolyai et Lobatchevsky (encore appelée hyperbolique), il est nécessaire de posséder la fonction exponen­tielle, qui ne fut construite qu’au cours des XVIIe et XVIIIe siècle, de Neper à Euler. La trigonométrie usuelle commence avec Hipparque de Nicée, la trigonométrie sphérique avec Menelaos, l’hyperbolique à la fin du XVIIIe (calculs de Lambert, anticipant les découvertes géométriques de B. et L.). C. V.

 

[1] Décelant notamment les interpolations dues à Théon d’Alexandrie, il entreprend de les distinguer du contexte. C’est F. Peyrard qui dénichera enfin, vers 1800, un manuscrit de tradition anté-théonienne, fort précieux pour l’établissement du texte.

[2] j’ajoute dans une note en fin d’article quelques compléments mathéma­tiques, dont le libellé du postulat, souvent reproduit de façon infidèle.

[3] Bien que n’ayant reçu que récemment la dignité de la nomina­tion, la méta-mathématique est au travail depuis l’Antiquité.

 

[4] Déjà Newton, dans ses Principia (1686), avait rangé sous le titre général d’« Axiomata » des prémisses de statut divers, mais cela n’implique pas qu’il tombe à proprement parler sous mes reproches.